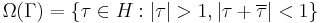Free regular set

In mathematics, a free regular set is a subset of a topological space that is acted upon disjointly under a given group action.

To be more precise, let X be a topological space. Let G be a group of homeomorphisms from X to X. Then we say that the action of the group G at a point 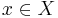$x\in X$ is freely discontinuous if there exists a neighborhood U of x such that 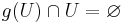$g(U)\cap U=\varnothing$ for all 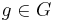$g\in G$ , excluding the identity. Such a U is sometimes called a nice neighborhood of x.

The set of points at which G is freely discontinuous is called the free regular set and is sometimes denoted by 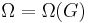$\Omega=\Omega(G)$ . Note that $\Omega$ is an open set.

If Y is a subset of X, then Y/G is the space of equivalence classes, and it inherits the canonical topology from Y; that is, the projection from Y to Y/G is continuous and open.

Note that 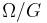$\Omega /G$ is a Hausdorff space.

Examples

The open set

$\Omega(\Gamma)=\{\tau\in H: |\tau|>1 , |\tau %2B\overline\tau| <1\}$

is the free regular set of the modular group $\Gamma$ on the upper half-plane H. This set is called the fundamental domain on which modular forms are studied.

Free regular set

Examples

See also